攻克 12 英寸晶圆旋涂 “边缘效应”,借助Ansys CFD仿真优化工艺参数,助力7nm 制程量产。

旋涂工艺仿真必要性及仿真方法
旋转涂胶作为半导体行业重要的制造工艺之一,通过硅片高速旋转产生的离心力实现光刻胶均匀分布,工艺要求胶膜厚度控制在0.5-1.5μm范围,误差需≤±0.01μm,直接影响后续光刻图形转移精度。随着硅片尺寸增大至300mm以上,该工艺面临材料利用率低(95%-98%被浪费)、三维结构涂覆不均等技术挑战。
wafer 转速、涂胶厚度与涂胶均匀性三者存在显著且相互耦合的相关性,其中wafer 转速是调控涂胶厚度的核心变量,在胶液粘度、滴胶量等参数固定时,转速升高会使离心力增大,更多多余胶液被甩出晶圆表面;但高速时虽能促进胶液快速铺展,但可能因晶圆边缘与中心的离心力差异引发 “边缘效应”,厚度需与转速协同匹配在合理范围。
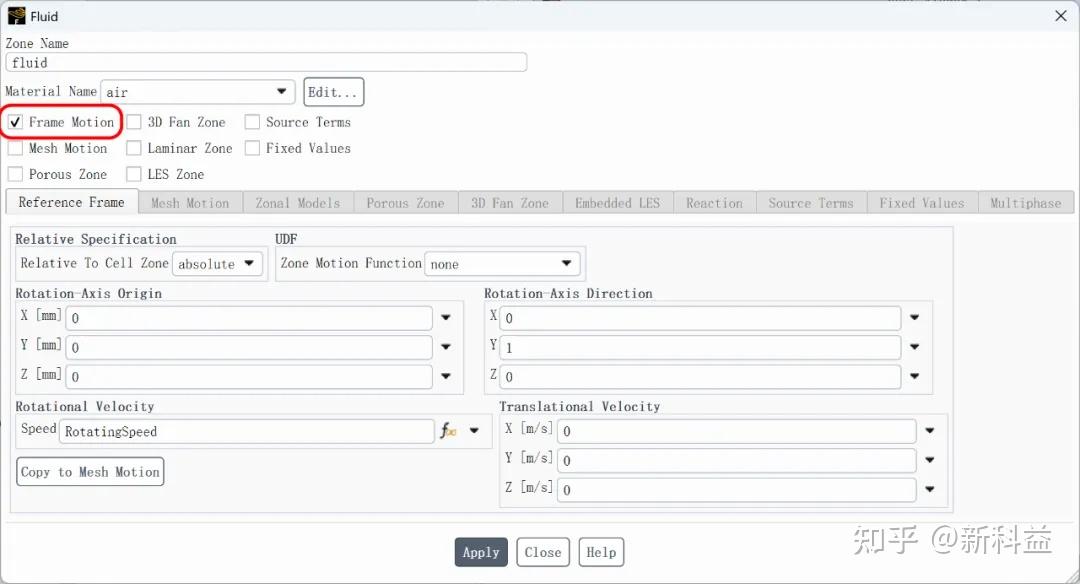
借助Ansys CFD仿真工具,通过模拟旋涂过程中流体的流动特性,可预测不同工艺参数(如转速、基板温度、流体粘度)对涂层均匀性的影响,优化工艺参数以提升涂层质量,提升良率。但是若使用VOF多相模型模拟涂层过程,当涂层厚度非常薄时,由于VOF模型无法捕捉小于网格分辨率的详细液 - 气界面,可能需要大网格模型;而使用Eulerian Wall Film(EWF)模型可使涂层模拟更简便,但该模型仅适用于3D,且与非共形界面不兼容。与VOF多相模型相比,EWF模型为旋涂工艺带来了显著优势。在模拟极薄涂层时,EWF模型能够克服VOF模型在捕捉详细液 - 气界面方面的局限,大大降低了对网格模型规模的要求,从而简化了涂层模拟过程,提高了模拟效率。
仿真模型描述及核心设置

采用Ansys Meshing生成hexa网格,体网格21万,圆柱流域顶部及侧面都预定义为压力出口pressure-outlet,底部为壁面wall,旋转轴为Y轴。
-
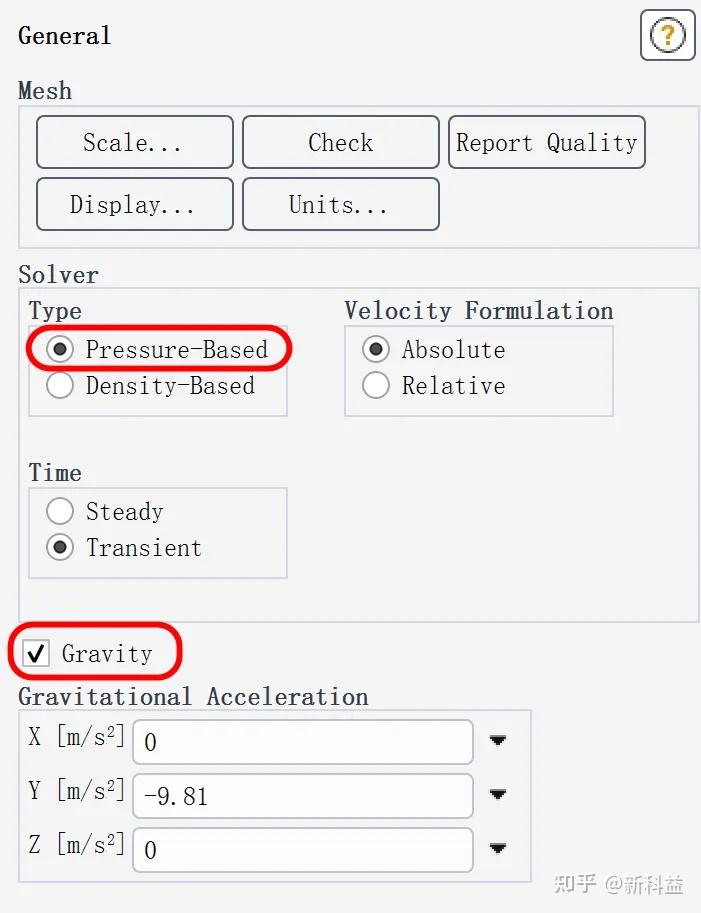
基于压力的瞬态求解器,开启重力项Gravity,湍流模型按照默认(SST K-W)
|
流体介质
|
名称
|
密度(kg/m3)
|
粘度(kg/m·s)
|
|
显影胶
|
SU-8胶
|
1200
|
0.5
|
|
气体
|
空气
|
1.225
|
1.789e-5
|
wafer 转速、涂胶厚度与均匀性关联紧密:固定胶液参数时,转速与厚度负相关(转速越高,厚度越薄);转速过低或过高均会降低均匀性,仅特定临界区间适配。且厚度过薄 / 过厚也会影响均匀性。
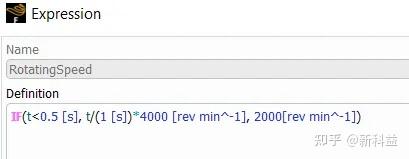
区域旋转速度通过表达式形式给出,可以用户自定义其转速随时间等变量的变化关系,如IF(t<0.5 [s], t/(1 [s])*4000 [rev min^-1], 2000[rev min^-1]),表示0.5s前,转速以一定斜率提升上来,0.5s及以后,持续以2000RPM旋转。通过设定的旋转速度评估在选定胶液的情况下对涂胶厚度以及均匀性的影响。
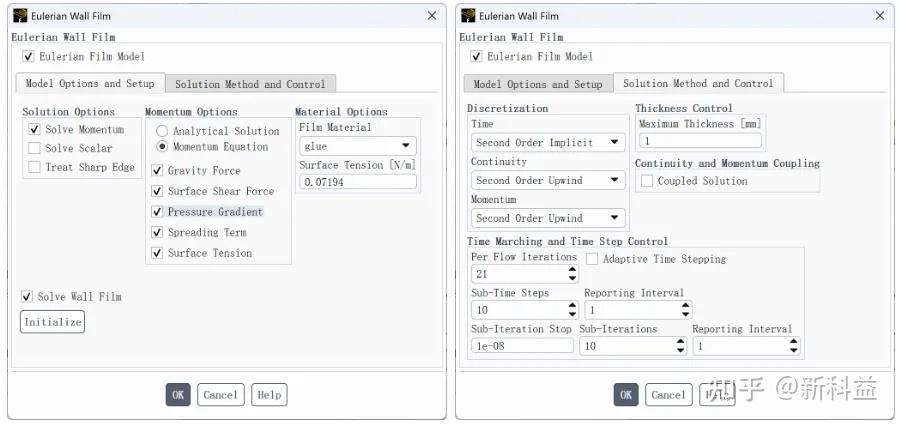
开启动量求解Solve Momentum,所有离散格式采用二阶格式seconde order implicit,膜的最大厚度为1mm,子时间步数为10,子时间报告间隔为1,子迭代次数为10,子迭代收敛标准为1e - 08,子迭代报告间隔为1。
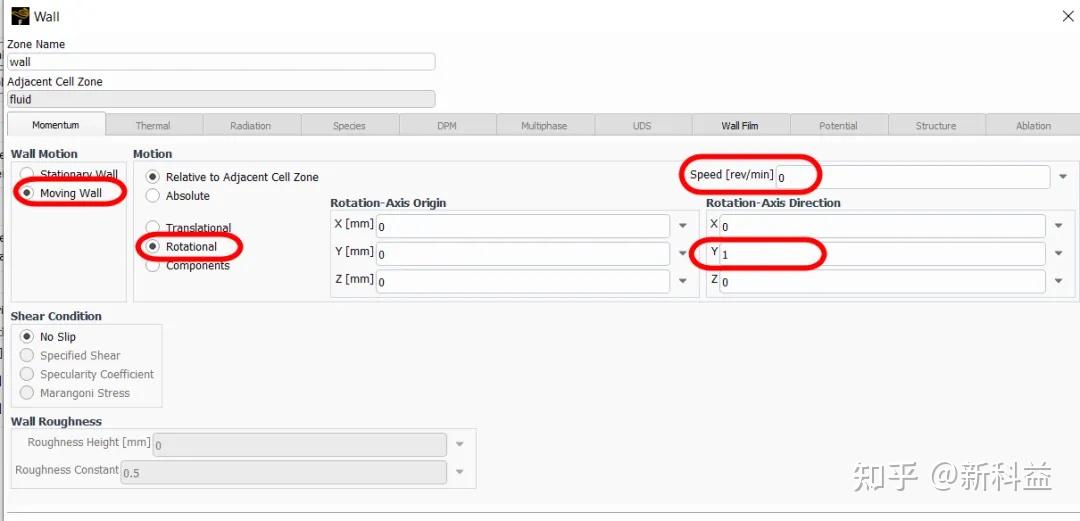
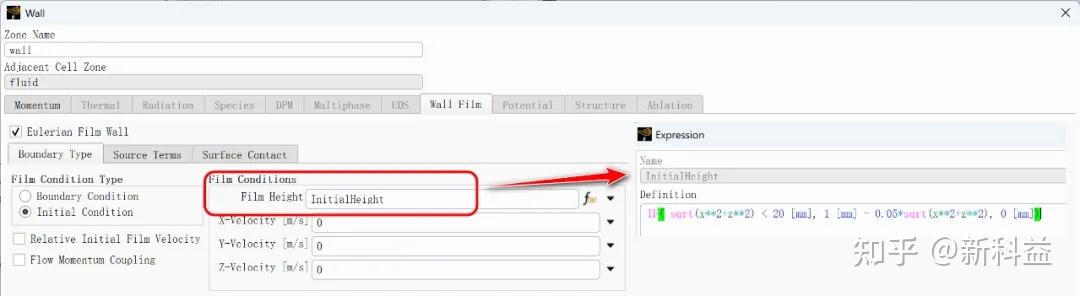
初始分布范围以及初始厚度,可以用户自定义其厚度随坐标位置等变量的变化关系,如IF( sqrt(x**2+z**2) < 20 [mm], 1 [mm] - 0.05*sqrt(x**2+z**2), 0 [mm]),表示当半径小于20mm,中心处膜最厚为1mm,膜厚度为一个随半径不断变小,当大于20mm时,没有液膜存在。
通过表达式方式,可以快速简便实现如右侧的液膜初始分布状态:
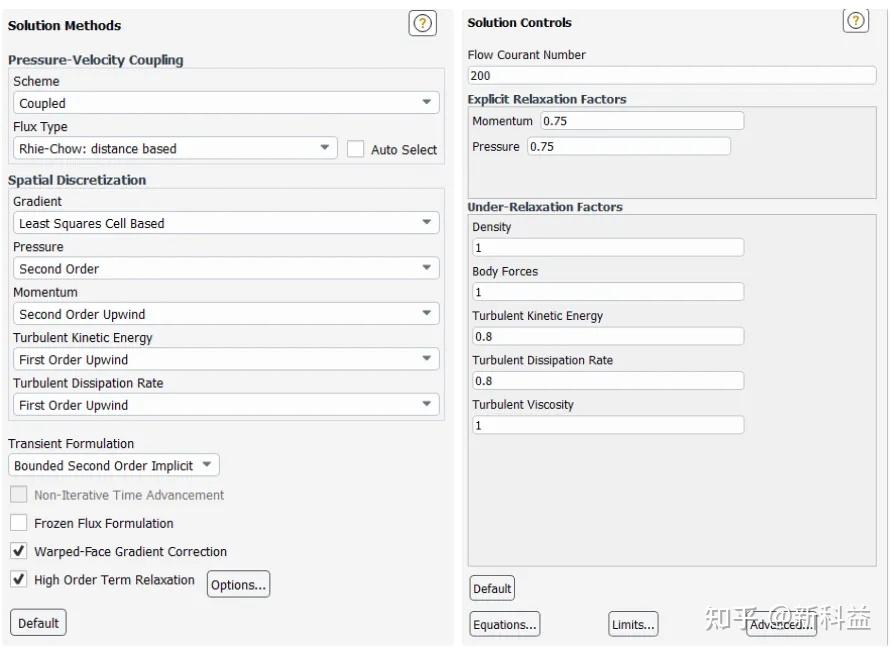
采用Coupled压力-速度耦合方案,梯度采用基于单元的最小二乘法,压力采用二阶格式,动量采用二阶迎风格式,湍动能和湍耗散率采用一阶迎风格式,对于瞬态,采用有界二阶隐式格式。
-
利用Execute Command功能预定义定制化输出特定后处理云图
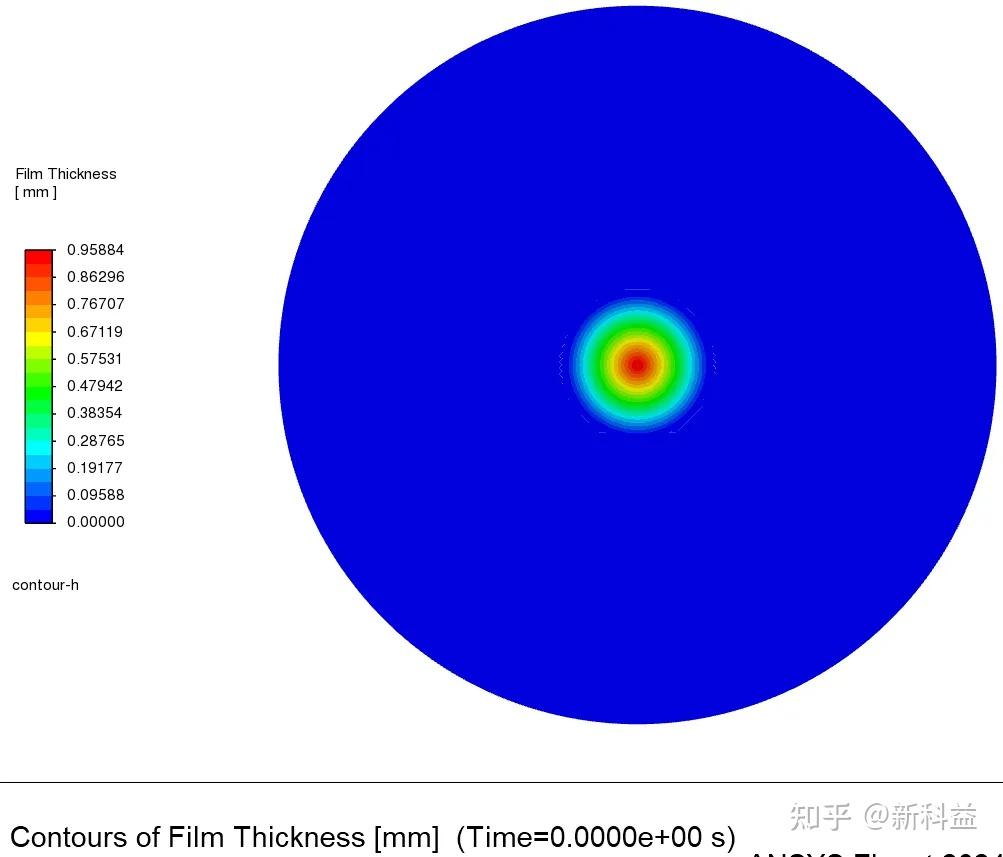
对于关注的旋涂表面薄膜厚度云图,预定义好其contour云图,命名微contour-h,如下图所示:
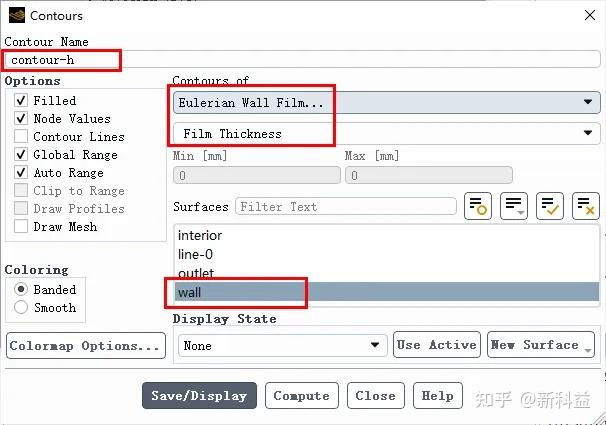
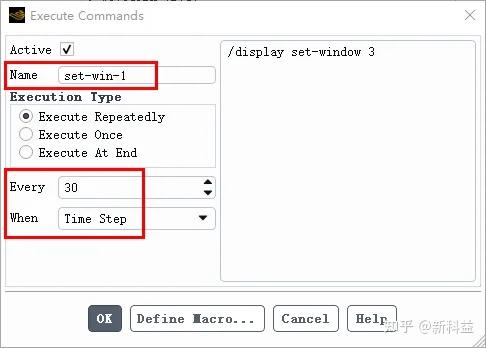
对于按照每30个time step保存输出薄膜厚度云图图片,预定义三个commands:
set-win-1:/display set-window 3 #生成新的窗口
display-contour:/display/objects/display contour-h #云图显示
set-view:/views/restore-view view-ss #设置视图显示
hardcopy-1 /display/save-picture thickness-%t.jpg #保存结果文件
如下图所示:
-
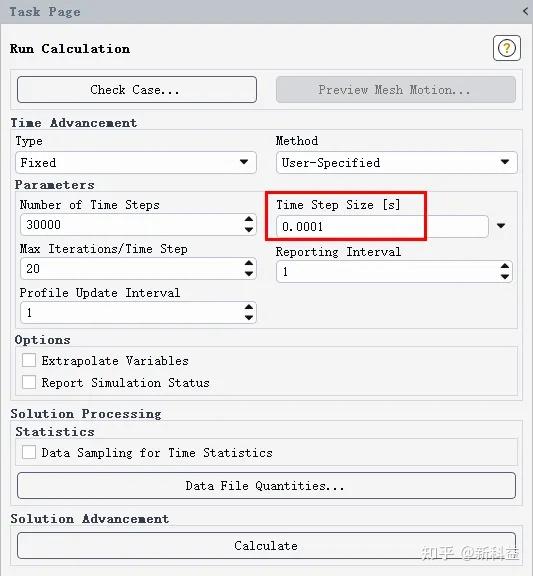
迭代计算:时间步长为0.0001[s],时间步数为50,000,每个时间步的最大迭代次数为20
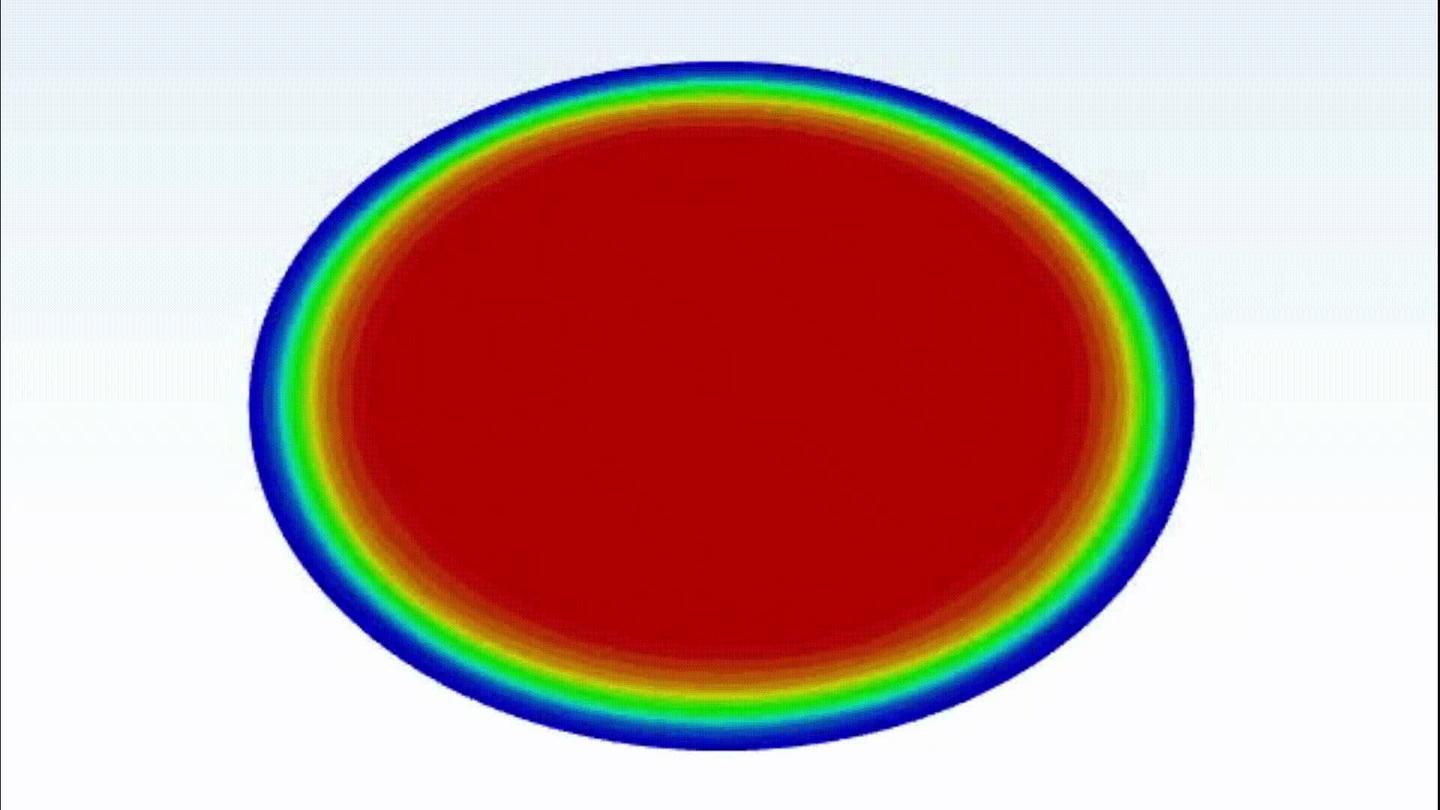
通过仿真得到了膜厚度的等值线动画(GIF)和膜厚度的XY绘图动画(GIF),直观展示了旋涂过程中膜厚度随时间的变化情况。
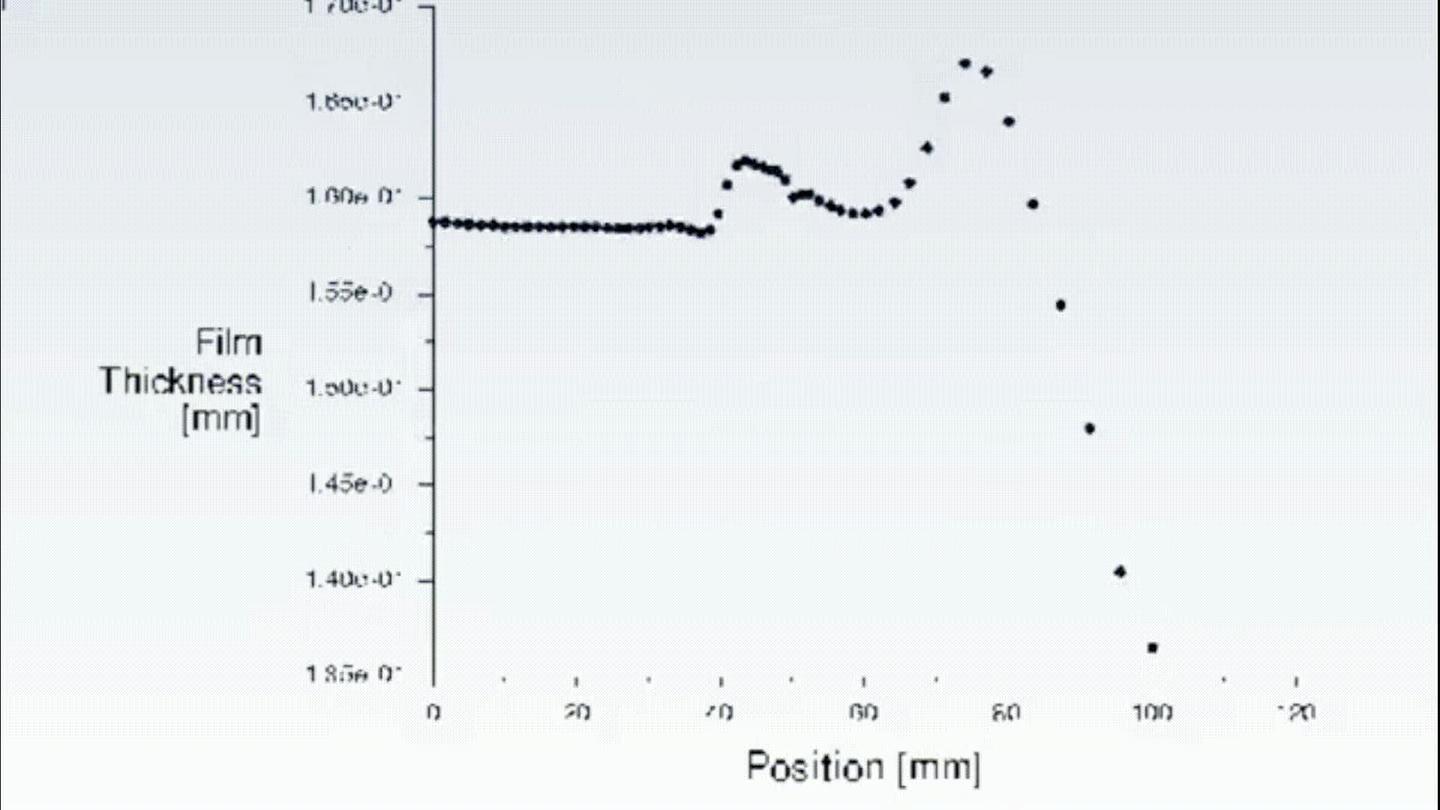
⭐多参数最佳匹配的仿真拓展
单一变量调整难以实现 “目标厚度与高均匀性” 的兼顾,必须通过 DOE(实验设计)开展多因素协同优化:通过设计转速(如 1000-6000rpm)、滴胶量(如 5-20μL)、胶液粘度(如 50-500cP)等关键参数的正交或响应面试验方案,结合统计分析(如方差分析、回归建模)量化各因素对厚度与均匀性的影响权重,最终筛选出 “转速 - 厚度 - 均匀性” 的最佳匹配组合(例如某正性光刻胶在 3200rpm 转速、12μL 滴胶量下,可稳定实现 1.0μm 目标涂胶厚度,且均匀性误差控制在 ±1.5% 以内),满足半导体工艺对胶层精度的严苛要求。
|